Les attaques sur les mots de passe - Les dictionnaires (2/2)

Le principe des attaques par dictionnaire est le suivant : l'être humain est prédictible et les attaquants le savent. Du coup, ils utilisent des dictionnaires de mots génériques ou spécifiques (prénoms, villes, métiers, acteurs, etc.).
Ensuite, il existe des logiciels capables d'augmenter le nombre de combinaisons en modifiant les mots de passe du dictionnaire avec des majuscules, des nombres et des caractères spéciaux.
Ensuite, il ne resta qu'à faire comme pour l'attaque par Brute Force, à savoir tester toutes les combinaisons grâce à notre liste.
Maintenant qu'on sait comment cela fonctionne, place aux calculs !
Entropie de Tr0ub4dor&3

Le mot de passe est composé d'un mot du dictionnaire, d'une majuscule, d'un chiffre, d'une substitution et d'un caractère spécial.
Le mot de passe a donc les possibilités suivantes :
- 32000 mots dans un dictionnaire français classique
- Une majuscule généralement en début ou en fin de mot
- Substitution d'une lettre avec un chiffre sur les voyelles ("O", "U", "A" et "U" de "troubador")
- 10 chiffres possibles
- 16 caractères spéciaux (j'ai pris ici les plus courants mais il y a plus où moins selon les sensibilités)
- 2 ordres possibles entre le chiffre et le caractère spécial
Cela nous donne le résultat suivant :
Le mot de passe fait 11 caractères de long donc, nous avons :
Il y a donc 2^27 bits possibilités.
Entropie de vaissellemyriadeparisroseau
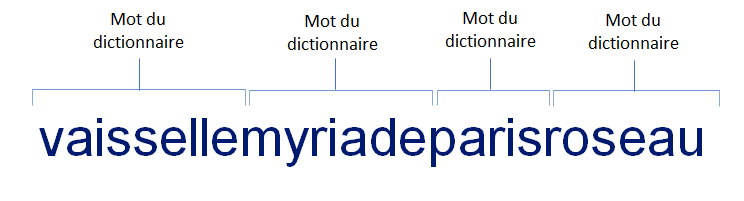
Pour le deuxième mot de passe, il n'y a que des mots donc cela nous donne la possibilité suivante :
- 32000 mots dans un dictionnaire français classique
Cela nous donne le résultat suivant :
Il y a donc 2^60 bits possibilités.
Résultats
Pour cet exemple, notre petit Hacker en herbe utilise tooujours son PC classique moyennement puissant équipe d'une carte graphique de type NVIDIA GeForce GTX 660.
Cette carte est capable de réaliser environ 2.000.000.000 de tests par seconde.
Pour nos deux mots de passe, le PC de notre Hacker pourrait cracker les deux mots de passe avec un temps de calcul de :
- Tr0ub4dor&3 : 67 ms
- vaissellemyriadeparisroseau : 18 ans
Outch ! On voit que cette technique est beaucoup plus efficace!
Conclusion
La technique de l'attaque par dictionnaire est trèèèès efficace ! Et surtout, on voit que notre mot de passe "complexe" ne l'est pas tant que ça.
C'est pour ça qu'il est généralement conseillé d'avoir un mot de passe long - pour éviter les attaques par brute force et aléatoire - pour éviter les attaques par dictionnaire !
Mais comment faire pour le retenir ?